
"Not only does God play dice, but... he sometimes throws them where they cannot be seen."
Conteúdo
Introdução
Um gerador de números pseudo-aleatórios(PRNG), também conhecido como gerador determinístico de bits aleatórios, é um algoritmo para gerar uma sequência de números cujas propriedades se aproximam das propriedades das seqüências de números aleatórios. A sequência gerada pelo PRNG não é verdadeiramente aleatória, porque é completamente determinada por um valor inicial, chamado semente do PRNG(ao qual pode incluir valores verdadeiramente aleatórios).
Embora as seqüências mais próximas de verdadeiramente aleatórias possam ser geradas usando geradores de números aleatórios de hardware, os geradores de números pseudo-aleatórios são importantes na prática por sua velocidade na geração de números e sua reprodutibilidade.
Aplicação
Muitas aplicações da aleatoriedade levaram ao desenvolvimento de diversos métodos diferentes para gerar dados aleatórios, dos quais alguns existem desde os tempos antigos, entre os mais conhecidos exemplos “clássicos” estão: O lançamento de dados, o lançamento de moedas, o embaralhamento de cartas de baralho, o uso de talos de Yarrow no I Ching, bem como inúmeras outras técnicas. Devido à natureza mecânica dessas técnicas, gerar um grande número de números aleatórios o suficiente (importante em estatística) exigia muito trabalho e/ou tempo.
Nos dias de hoje existem vários métodos computacionais para geração de números pseudo-aleatórios. Todos ficam aquém do objetivo da verdadeira aleatoriedade, embora possam atender, com sucesso variável, a alguns dos testes estatísticos da aleatoriedade destinados a medir o quão imprevisíveis são seus resultados (ou seja, em que grau seus padrões são discerníveis). Isso geralmente os torna inutilizáveis para aplicações como criptografia. No entanto, também existem geradores de números pseudo-aleatórios criptograficamente seguros (CSPRNG) cuidadosamente projetados, com recursos especiais projetados especificamente para uso em criptografia.
Aplicações Práticas e Uso
Os geradores de números aleatórios possuem aplicações em diversos campos:
- Apostas
- Amostras Estatísticas
- Simulações Computacionais
- Algoritmos de Machine Learning
- Criptografia
- Games
A geração de números pseudo-aleatórios é uma tarefa importante e comum na programação de computadores. Embora a criptografia e certos algoritmos numéricos exijam um grau muito alto de aleatoriedade aparente, muitas outras operações precisam apenas de uma quantidade modesta de imprevisibilidade.
Alguns exemplos simples que podemos considerar:
- Escolher uma “citação aleatória do dia” dentre uma lista de citações
- Determinar para que lado um adversário controlado por computador pode se mover em um jogo de computador
- Embaralhar uma lista de números ou cards
Formas mais fracas de aleatoriedade são usadas em algoritmos de hash e na criação de algoritmos de busca e ordenação amortizados.
O Módulo Random
A biblioteca padrão do Python fornece um módulo chamado random que oferece um conjunto de funções para gerar números aleatórios. Python utiliza um gerador de números pseudo-aleatórios popular e robusto chamado Mersenne Twister.
Quase todas as funções do módulo dependem da função básica random(), que gera um float aleatório uniformemente no intervalo semi-aberto [0.0, 1.0). O gerador Mersenne Twister produz floats de precisão de 53 bits e possui um período de 2**19937-1. A implementação subjacente em C é rápida e segura para threads. O Mersenne Twister é um dos geradores de números aleatórios mais amplamente testados existentes. No entanto, sendo completamente determinístico, não é adequado para todos os fins e é totalmente inadequado para fins criptográficos.
Para utilizarmos o módulo random você precisa importá-lo no seu programa e estará pronto para o uso, não há necessidade de instalarmos uma vez que ele já vem embutido diretamente na linguagem Python. Vamos então usar a seguinte instrução para importar o módulo random em nosso projeto:
import randomUtilizaremos a função dir() para examinarmos os atributos e métodos disponíveis no módulo random:
print(dir(random))Obteremos como output uma lista Python contendo diversos atributos e métodos, destacamos a seguir os mais usados e importantes:
| Método | Descrição |
|---|---|
| seed() | Inicializa o gerador de números aleatórios |
| getstate() | Retorna o estado interno atual do gerador de números aleatórios |
| setstate() | Restaura o estado interno do gerador de números aleatórios |
| getrandbits() | Retorna um número representando os bits aleatórios |
| randrange() | Retorna um número aleatório entre o intervalo especificado |
| randint() | Retorna um número aleatório entre o intervalo especificado |
| choice() | Retorna um elemento aleatório da sequência especificada |
| choices() | Retorna uma lista com uma seleção aleatória da sequência especificada |
| shuffle() | Toma uma sequência e retorna a sequência em uma ordem aleatória |
| sample() | Retorna uma determinada amostra de uma sequência |
| random() | Retorna um número float aleatório entre 0 e 1 |
| uniform() | Retorna um número float aleatório entre dois parâmetros fornecidos |
Detalhes sobre cada função podem ser encontrados na Documentação random, podemos também inspecionar o código-fonte do módulo através do seguinte repositório: random.py
Semeando o Gerador de Números Aleatórios
O gerador de números pseudo-aleatórios é uma função matemática que gera uma sequência de números “quase” aleatórios.
É necessário um parâmetro para iniciar a sequência, denominada semente. A função é determinística, ou seja, dada a mesma semente, ela sempre produzirá a mesma sequência de números. A escolha da semente não importa.
A função seed() irá propagar o gerador de números pseudoaleatórios, assumindo um valor inteiro como argumento, como 1 ou 8 por exemplo. Se a função seed() não for chamada antes do uso da aleatoriedade, o padrão é usar a hora atual do sistema em milissegundos da época (1970).
Vejamos o exemplo abaixo, que demonstra a semeadura do gerador de números pseudoaleatórios, gerando alguns números aleatórios e mostrando que a nova propagação do gerador resultará na mesma sequência de números gerados.
# Semeando o gerador de números aleatórios
random.seed(8)
# Gerando 5 números aleatórios
for _ in range(5):
print(random.random())
# Vamos agora resetar a semente com o mesmo valor
random.seed(8)
# Gerando 5 números aleatórios com list comprehensions
n = [random.random() for _ in range(5)]
print(n)A execução dos exemplos semeia o gerador de números pseudo-aleatórios com o valor 8, gera 5 números aleatórios, reinicia o gerador e mostra que os mesmos cinco números aleatórios são gerados novamente, demonstrando que esse experimento pode ser reproduzido.
0.2267058593810488
0.9622950358343828
0.12633089865085956
0.7048169228716079
0.08518526805075266
[0.2267058593810488,
0.9622950358343828,
0.12633089865085956,
0.7048169228716079,
0.08518526805075266]Pode ser útil controlar a aleatoriedade, definindo a semente para garantir que seu código produz o mesmo resultado a cada vez, como em um modelo de produção.
Gerando Números Aleatórios
A função random() é a função mais básica do módulo random, praticamente todas as funções do módulo random dependem dela. Ela é capaz de nos retornar um número floating-point no intervalo [0.0, 1.0). Dessa vez vamos testá-la sem uma semente:
numero = random.random() # float aleatório: 0.0 <= x < 1.0
print(f'Geramos o número: {round(numero,4)}')Veja que utilizamos também a função round() para arredondar o número obtido para 4 casas depois da vírgula. Imediatamente nos é trazido o seguinte output:
Geramos o número: 0.1231Obtivemos o número 0.1231, como dessa vez não há uma semente, é muito provável que você obtenha um número diferente.
A função uniform(a,b) retorna um número floating-point aleatório N, de modo que a <= N <= b para a <= b e b <= N <= a para b < a. Para melhor compreensão, vejamos um exemplo:
for _ in range(5):
valor = random.uniform(1,5)
print(valor)Ao executar o código obteremos o seguinte output:
2.4948768726321906
2.1987279202088144
3.89831254110623
2.684307463712701
4.6945137300543855Veja que fomos capazes de gerar cinco números aleatórios distribuídos uniformemente no intervalo especificado por nós.
Gerando Números Aleatórios Inteiros
Os métodos randint() e randrange() nos permitem gerarmos números inteiros aleatórios, vejamos alguns exemplos deles:
- randint(a,b): Retorna um inteiro aleatório N de tal forma que
a <= N <= b.
inteiro = random.randint(1,10)
print(f'Gerando um número aleatório entre 1 e 10: {inteiro}')Nos é trazido o seguinte output:
Gerando um número aleatório entre 1 e 10: 10- randrange(start, stop, step): Retorna um elemento aleatoriamente escolhido do intervalo
range(start, stop, step)o padrão de argumento posicional corresponde ao da funçãorange().
n = random.randrange(0, 10, 2)
print(f'Gerando um número aleatório no range(0, 10, 2): {n}')Nos é trazido o seguinte output:
Gerando um número aleatório no range(0, 10, 2): 4Observe que iremos obter somente números pares até 8, uma vez que 10 não será incluído em nosso intervalo.
Gerando Valores Gaussianos Aleatórios
Valores aleatórios de floating-point podem ser obtidos de uma distribuição Gaussiana usando a função gauss().
Essa função usa dois argumentos que correspondem aos parâmetros que controlam o tamanho da distribuição, especificamente a média e o desvio padrão.
O exemplo abaixo gera 5 valores aleatórios extraídos de uma distribuição Gaussiana com uma média de 4 e um desvio padrão de 2.
for _ in range(5):
print(random.gauss(4,2))Ao executarmos o exemplo, teremos o seguinte output:
0.6384362151512204
5.108313708726303
2.766667041131024
6.115255903840948
6.506724074980704Perceba que os parâmetros utlizados não são os limites dos valores e que a dispersão dos valores será controlada pelo formato de sino(Bell Shape) da distribuição, neste caso, proporcionalmente provavelmente acima e abaixo de 4.
Selecionando Aleatoriamente um Item de uma Lista
Imagine que temos uma lista de números e queremos selecionar aleatoriamente um número dessa lista. Vejamos como podemos lidar com essa situação:
numeros = [1,3,5,7,9,11,13,27,33,55,128]
selecao = random.choice(numeros)
print(f'O número escolhido da lista {numeros} é -> {selecao}')Observe que cada vez que executarmos o código será selecionado um número diferente da lista.
Agora considere que temos uma lista de cores e desejamos selecionar N vezes um valor dessa lista e guardá-los em uma nova lista:
cores = ['preto','branco']
selecao = random.choices(cores, k=12)
print(f'As cores escolhidas da lista {cores} é -> {selecao}')Atualmente cada cor é igualmente provável de ser selecionada, porém podemos configurar o peso(weights) das cores para tornar nossa seleção tendenciosa, nesse caso vamos aumentar consideravelmente a chance de escolhermos a cor preta:
cores = ['preto','branco']
selecao = random.choices(cores, weights=[10,1], k=12)
print(f'As cores escolhidas da lista {cores} é -> {selecao}')Selecionando Amostras Únicas
Suponha que temos um baralho com 52 cartas e desejamos selecionar uma amostra de 5 cartas desse deck:
- o método
sample(populacao,k)retorna uma lista de elementos únicos escolhidos de uma população. - A contagem dos elementos totais depende do tamanho de
k - A
populacaopode ser uma list, set, tuple, ou qualquer sequência
Considere o seguinte exemplo ilustrativo:
deck = tuple(range(1,53))
amostra = random.sample(deck,5)
print(f'Foi escolhida a seguinte amostra: {amostra}')A cada execução serão selecionadas amostras de cartas diferentes, sem que haja repetição.
Embaralhando Itens de uma Lista
A função shuffle() nos permite embaralhar ou randomizar uma lista. Importante lembrar que a função shuffle() embaralha a lista in-place. Considere o seguinte conjunto de músicas:
musicas = ['Valhalla','Octvarium','Comfortably Numb']
random.shuffle(musicas)
print(f'Lista embaralhada é {musicas}')Nos será retorna o seguinte output:
Lista embaralhada é ['Octvarium', 'Valhalla', 'Comfortably Numb']Para obter mais detalhes sobre o método shuffle(), você pode visitar o seguinte Guia.
Números Aleatórios com NumPy
As rotinas de números aleatórios de Numpy produzem números pseudo-aleatórios usando combinações de um BitGenerator para criar sequências e um Gerador para usar essas sequências para amostrar em diferentes distribuições estatísticas.
Desde a versão 1.17.0 do Numpy, o gerador pode ser inicializado com vários BitGenerators diferentes. Ele expõe muitas distribuições de probabilidade diferentes.
É importante lembrarmos que a biblioteca Numpy não está acoplada no Python, portando devemos instalar ela através de um gerenciador de pacotes, nesse caso vamos utilizar o pip:
pip install numpyAgora já é possível importarmos numpy em nosso projeto:
import numpy as np
print(help(np))Veja que nos será trazido informações essenciais sobre o que a biblioteca numpy é capaz de prover:
- Um objeto array de itens homogêneos arbitrários
- Operações matemáticas rápidas sob arrays
- Álgebra Linear, Transformadas de Fourier, Geração de Números Aleatórios
Gerando Números Aleatórios com NumPy
A função rand() nos retorna valores aleatórios em uma determinada forma.
Crie um array da forma especificada e preencha-a com amostras aleatórias a partir de uma distribuição uniforme em [0, 1).
import numpy.random as np
print(np.rand()) # 0.8508269139072056Especificando as dimensões nos trará um Array(1 Dimensão) ou até mesmo uma Matriz(2 Dimensões).
Array de três números
print(np.rand(3))
# array([0.38094113, 0.06593635, 0.2881456 ])Matriz 2x2
print(np.rand(2,2))
# array([[0.90959353, 0.21338535],
# [0.45212396, 0.93120602]])Um array de números inteiros aleatórios pode ser gerado usando a função NumPy randint(). Essa função receberá três argumentos, o limite inferior do intervalo, o limite superior do intervalo e o número de valores inteiros a serem gerados ou o tamanho do array.
Vamos ver um exemplo:
array_numeros = np.randint(0,10,8)
print(array_numeros) # [5 0 0 2 8 9 6 4]Executando o exemplo nos traz uma lista com 8 números entre 0 e 9.
Distribuição Normal
A função normal() retira amostras aleatórias de uma distribuição normal(gaussiana).
A função densidade de probabilidade da distribuição normal, derivada pela primeira vez por De Moivre e 200 anos depois por Gauss e Laplace independentemente, é freqüentemente chamada de curva de sino devido à sua forma característica.
A função normal espera os parâmetros:
- loc: floating-point ou array de floats | Média(centro) da distribuição
- scale: floating-point ou array de floats | Desvio padrão (espalhamento ou comprimento) da distribuição
- size: inteiro ou tupla de inteiros, opcional | Forma de saída. Se a forma especificada for, por exemplo,
(m, n, k), entãom * n * kamostras serão coletadas. Se o tamanho for None(padrão), um único valor será retornado se loc e scale forem ambos escalares.
Vejamos alguns exemplos:
np.normal() # 0.5931281518098956Gerando cinco números:
np.normal(size=5)
# array([0.47545955,-0.57327425,-0.59239159,0.03916865,-0.1948815])Consideramos agora a densidade de probabilidade para a distribuição gaussiana, que possui a respectiva fórmula:
Onde mu é a média e sigma o desvio padrão. O quadrado do desvio padrão é chamado de variância.
A função tem seu pico na média e seu “espalhamento” aumenta com o desvio padrão (a função atinge 0,607 vezes o seu máximo em e ). Isso implica que é mais provável que a função normal() retorne amostras próximas da média, em vez de distantes.
Para ilustrar melhor essa ideia, vejamos o seguinte exemplo:
import matplotlib.pyplot as plt
import numpy as np
# define a média e desvio padrão
mu, sigma = 0, 0.1
# Gera mil amostras
amostras = np.random.normal(mu, sigma, 1000)
# Projeta o gráfico das amostras e a função de Gauss
plt.figure(figsize=(11,8))
plt.grid()
plt.hist(amostras, 40, density=True, color='gray', edgecolor='black')
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
np.exp( - (bins - mu)**2 / (2 * sigma**2)),
linewidth=2, color='blue')
plt.show()Vamos obter o seguinte gráfico:
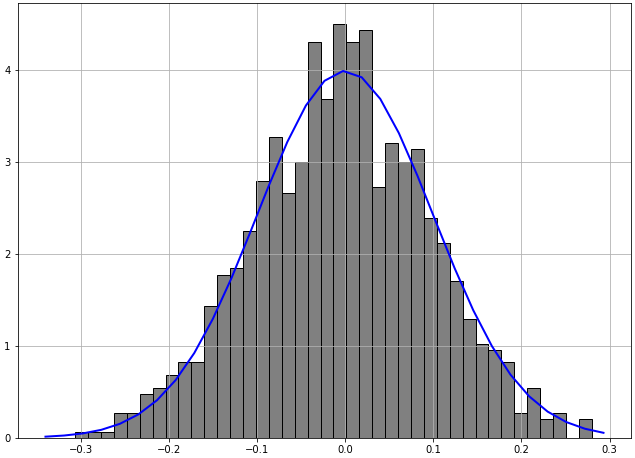
Distribuições normais são importantes em estatística e são frequentemente usadas nas ciências naturais e sociais para representar variáveis aleatórias com valor real cujas distribuições não são conhecidas. Sua importância é parcialmente devido ao teorema do limite central. Ele afirma que, sob algumas condições, a média de muitas amostras (observações) de uma variável aleatória com média e variância finitas é ela própria: uma variável aleatória cuja distribuição converge para uma distribuição normal à medida que o número de amostras aumenta.
Conclusão
Neste tutorial estudamos a respeito dos geradores de números pseudo-aleatórios e descobrimos como podemos gerar números aleatórios através da linguagem Python, bem como vimos aplicações dos números aleatórios que podem nos ajudar a resolver problemas práticos.
Para expandir seu conhecimento sobre números aleatórios ainda mais, considere explorar as bibliotecas:
- secrets: O módulo secrets é usado para gerar números aleatórios criptograficamente fortes, adequados para gerenciar dados como senhas, autenticação de conta, tokens de segurança e segredos relacionados.
- uuid: O módulo uuid fornece objetos UUID imutáveis e as funções uuid1(), uuid3(), uuid4(), uuid5() para gerar UUIDs das versões 1, 3, 4 e 5, conforme especificado na RFC 4122.
Bons estudos!
Referências
- Pseudorandom generator
- Pseudorandom number generator
- Python Random Module
- How to use the Random Module in Python
- Python Random Module W3S
- Python Random Module to Generate random numbers and Data
- How to Generate Random Numbers in Python
- random - Generate pseudo-random numbers
- Normal Distribution
- NumPy Package