Explorando o Conjunto Julia com Python

Introdução

O Conjunto Julia recebeu o nome do matemático francês Gaston Julia, que investigou suas propriedades no começo do século XX.

Julia estudou expressões polinomiais racionais de vários graus, neste guia focaremos especificamente na família de conjuntos que são gerados pela fórmula quadrática especial:

Em que: z representa uma variável na forma a + ib (sendo a e b números reais) que pode assumir todos os valores no plano complexo. A quantidade c também é definida como um número complexo, mas, para qualquer conjunto de Julia, ele é mantido constante (portanto, é chamado de parâmetro), em outras palavras, há um número infinito de conjuntos Julia, cada um definido para um determinado valor de c.

Usada uma vez, a expressão simples f(z) = z² + c tem pouco potencial para criar algo interessante - é apenas iterando repetidamente que o conjunto de Julia pode ser definido.

Quando a saída da expressão f(z) é retornada à expressão como um novo valor de z, isso é chamado de iteração, um tipo de processo de feedback. Assim, para qualquer n iterações:

Cada novo valor calculado de f(z) se torna o valor de entrada subsequente de z através do loop de feedback.

Para qualquer valor inicial de z, digamos por exemplo z0, há duas possibilidades para o que acontecerá com os valores iterados de f(z):

• À medida que n aumenta em direção ao infinito: f(z) pode continuar a crescer sem limites ou permanecerá limitado. Dizem-se que os pontos z0 no plano complexo que não ficam delimitados com iterações sucessivas de f(z) estão no conjunto de escape Ec.
• Todos os outros pontos do plano complexo permanecem limitados quando n é levado ao infinito - eles são denominados prisioneiros e dizem estar no conjunto de prisioneiros Pc definido para um determinado c.

Todos os pontos devem estar em um ou no outro conjunto.

O limite comum entre o conjunto escape e o conjunto de prisioneiros é chamado de Conjunto Julia, definido para um valor particular de c. O raio do limite r(c) = max(|c|, 2) fornece um critério de teste útil para a implementação no computador. Se uma órbita zk exceder o raio limiar r(c), é certo que a órbita escapará em direção ao infinito e, portanto, o ponto de partida estará no conjunto de escape (Peitgen et al. 1992 p. 794).

Conjuntos Julia Conectados vs Desconectados

Dependendo do valor de c selecionado, o Conjunto Julia resultante pode ser conectado ou desconectado - na verdade, totalmente conectado ou totalmente desconectado.

O matemático Mandelbrot, chamou os conjuntos Julia desconectados de ”dust of points”, ou “Fatou Dust”(em homenagem a Pierre Fatou 1878-1929). Este é um termo lógico, uma vez que um conjunto de Julia desconectado consiste em pontos individuais no plano complexo que, como poeira(dust) esparramada em uma folha, não estão conectados a nenhum outro. Outro termo usado para descrever um conjunto de Julia desconectado é “Cantor Dust”(Peitgen et al. 1992, p. 798).

Implementação em Python

Para que tenhamos uma melhor ideia de como o Conjunto Julia funciona, vamos considerar o seguinte exemplo escrito em Python

import matplotlib.pyplot as plt
import numpy as np
 
m = 600 # Largura
n = 395 # Altura
s = 2800 # Escala
c = -0.162 + 1.04j

x = np.linspace(-m / s, m / s, num=m).reshape((1, m))
y = np.linspace(-n / s, n / s, num=n).reshape((n, 1))
Z = np.tile(x, (n, 1)) + 1j * np.tile(y, (1, m))

C = np.full((n, m), c)
M = np.full((n, m), True)
N = np.zeros((n, m))

for i in range(70):
    Z[M] = Z[M] * Z[M] + C[M]
    M[np.abs(Z) > 2] = 0
    N[M] = i
 
fig = plt.figure()
fig.set_size_inches(m / 100, n / 100)
ax = fig.add_axes([0, 0, 1, 1])
plt.imshow(N, cmap='twilight_shifted')
plt.savefig('julia_set.png')

Para calcular o polinômio para todos os pixels de uma imagem ao mesmo tempo, criamos uma matriz Z e, em seguida, executamos a computação.

Em que * significa a multiplicação de matrizes elemento por elemento. c é uma constante complexa e J é a matriz unitária com as mesmas dimensões que Z. Uma matriz unitária é uma matriz com todos os elementos iguais a 1.

Cada elemento da matriz Z deve ser inicializado na coordenada do pixel no plano complexo que ele representa.

Em seguida executamos a computação das iterações e salvamos a imagem gerada pelo algoritmo.

Exemplos de Imagens Geradas

c = -0.8 + 0.156i

c = -0.8i

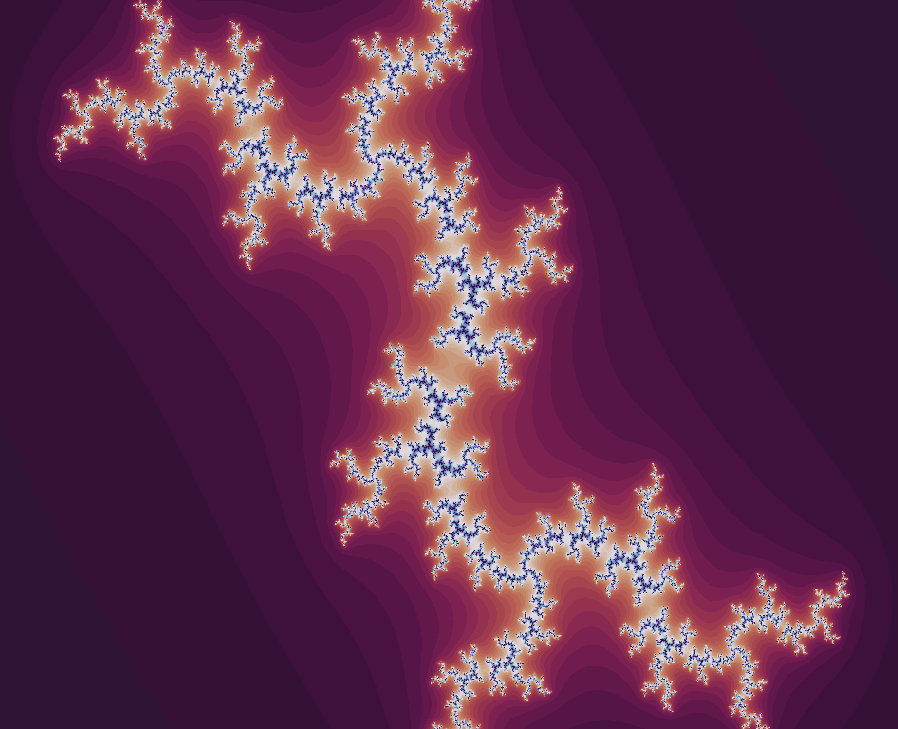
c = 1 - φ

c = -0.835 -0.2321i

c = 0.285 + 0i

c = -0.162 + 1.04i

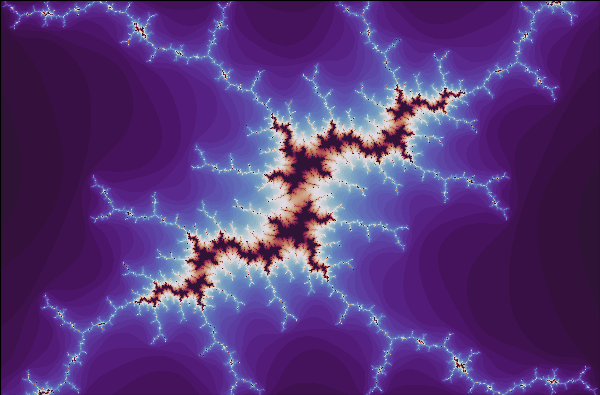
Conclusão

Estudamos nesse breve guia as propriedades matemáticas que nos levam à construção de imagens fractais, assim como a implementação de um simples script Python capaz de gerar essas imagens em diferentes escalas, cores e formas.

Você pode consultar as referências para conhecer os diferentes valores que c pode assumir.

Para mais materiais de matemática, você pode visitar: Matemática com Python

Bons estudos!

Referências

• Julia Set
• 8-bit Julia Set Art in Python
• Wolfram MathWorld
• Understanding Julia and Mandelbrot Sets
• Julia Jewels: An Exploration of Julia Sets
• How to Compute Colorful Fractals