O Algoritmo Quick Sort

Introdução

Quick Sort é um algoritmo de sorting/ordenação altamente eficiente no qual baseia-se no particionamento do array de dados em arrays menores, ele é um algoritmo de Divide and Conquer.

Foi Desenvolvido pelo cientista da computação Tony Hoare em 1959 e publicado em 1961, ainda é um algoritmo comumente usado para sorting. Quando bem implementado, pode ser cerca de duas ou três vezes mais rápido que seus principais concorrentes, merge sort e heap sort.

Ele funciona selecionando um elemento ‘pivot’ do array e particionando os outros elementos em dois subarrays, dependendo se são menores ou maiores que o pivot. Os subarrays são então ordenados recursivamente. Isso pode ser feito in-place, exigindo pequenas quantidades adicionais de memória para realizar o procedimento de sorting.

A análise matemática em questão de complexidade de tempo do Quick Sort mostra que, em média, o algoritmo faz comparações O(nlogn) para ordenar n itens. Na pior das hipóteses, faz comparações de O(n²), embora esse comportamento seja raro.

Procedimento

O Algoritmo Quick Sort funciona da seguinte maneira:

• Escolher um elemento do array que será chamado de pivot.
• Particionar: reordenar o array para que todos os elementos com valores menores que o pivot venham antes do pivot, enquanto todos os elementos com valores maiores que o pivot venham depois dele. Após essa partição, o pivot está em sua posição final. Isso é chamado de operação de partição.
• Aplicar recursivamente as etapas acima ao subarray de elementos com valores menores e separadamente ao subconjunto de elementos com valores maiores.

Uma vez que estamos lidando com recursão, é necessário um base case simples: um cenário final que não usa recursão para produzir uma resposta.

Recursão é o processo pelo qual um procedimento passa quando uma das etapas do procedimento envolve a invocação do próprio procedimento. Um procedimento que passa por recursão é considerado ‘recursivo’.

Quando um procedimento é definido como tal, isso cria imediatamente a possibilidade de um loop sem fim; a recursão só pode ser usada adequadamente em uma definição se a etapa em questão for ignorada em certos casos, para que o procedimento possa ser concluído.

Implementação em Python

Para que consigamos compreender melhor o Quick Sort, vamos considerar uma simples implementação em Python, versão menos comum, não in-place do Quicksort que usa espaço O(n) para armazenamento de trabalho e pode implementar uma ordenação estável.

O armazenamento de trabalho permite que o array de entrada seja particionada facilmente de maneira estável e depois copiada de volta para o array de entrada para chamadas recursivas sucessivas.

from random import choice

def quick_sort(array):
    menores, maiores, lista_pivot = [], [], []
    if len(array) < 2:
        return array
    else:
        pivot = choice(array)
        for i in array:
            if i < pivot:
                menores.append(i)
            elif i > pivot:
                maiores.append(i)
            else:
                lista_pivot.append(i)
        menores = quick_sort(menores)
        maiores = quick_sort(maiores)
        return menores + lista_pivot + maiores
 
lista = [51,95,66,72,42,38,39,41,15]
list_ordenada = quick_sort(lista)
print(list_ordenada)

1. Observe que estamos definindo três listas Python: menores, maiores e lista_pivot.
2. Definimos um base case: se o tamanho do array de input for menor que 2, então retornamos ele.
3. Escolhemos um pivot de maneira aleatória, percorremos todos os elementos do array e os comparamos com o pivot: os menores são destinados ao array de menores, e os maiores para o de maiores e o pivot para a lista_pivot.
4. Chamamos novamente a função quick_sort() e repetimos o procedimento até que o array esteja ordenado.

Tecnicamente, o algoritmo quick sort segue as etapas abaixo:

1. Faça qualquer elemento como pivot.
2. Particionar o array com base no pivot.
3. Aplicar o quick sort na partição esquerda recursivamente.
4. Aplicar o quick sort na partição direita recursivamente.

Na ilustração a seguir, fazemos o procedimento de partição do array com base no primeiro pivot selecionado:

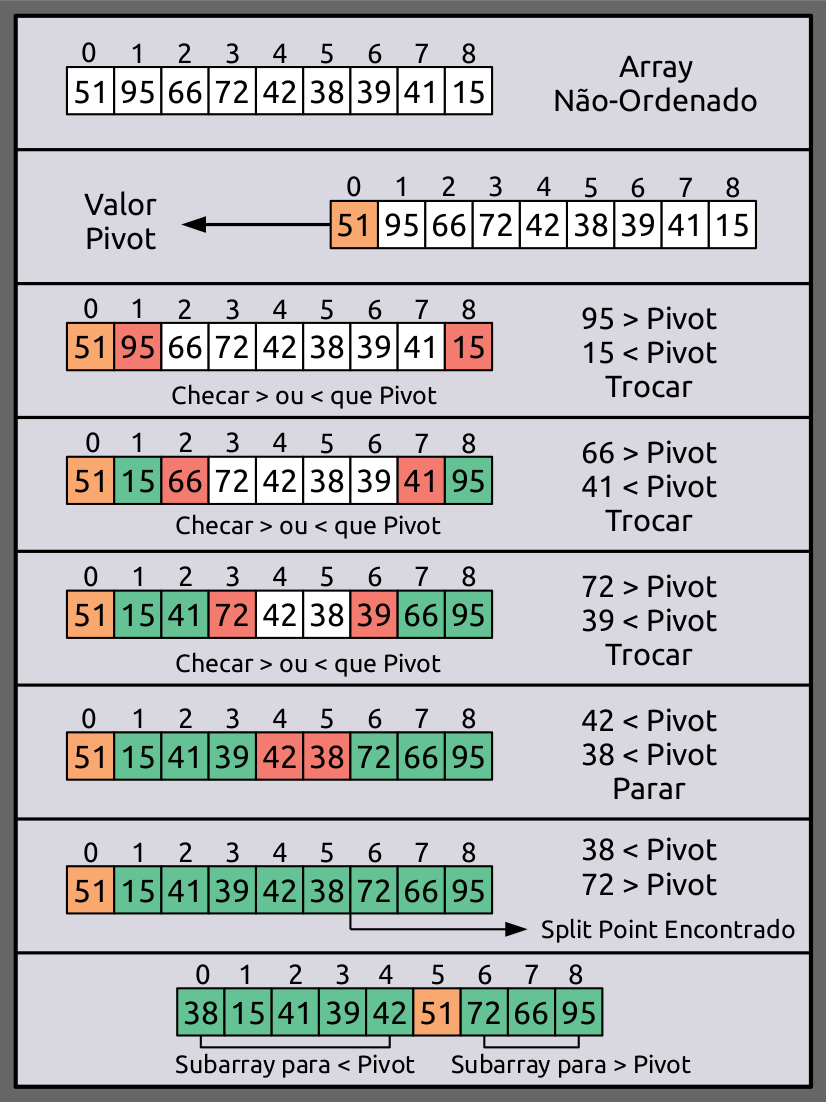
Já na seguinte ilustração, aplicamos o algoritmo quick sort recursivamente em todas as partições:

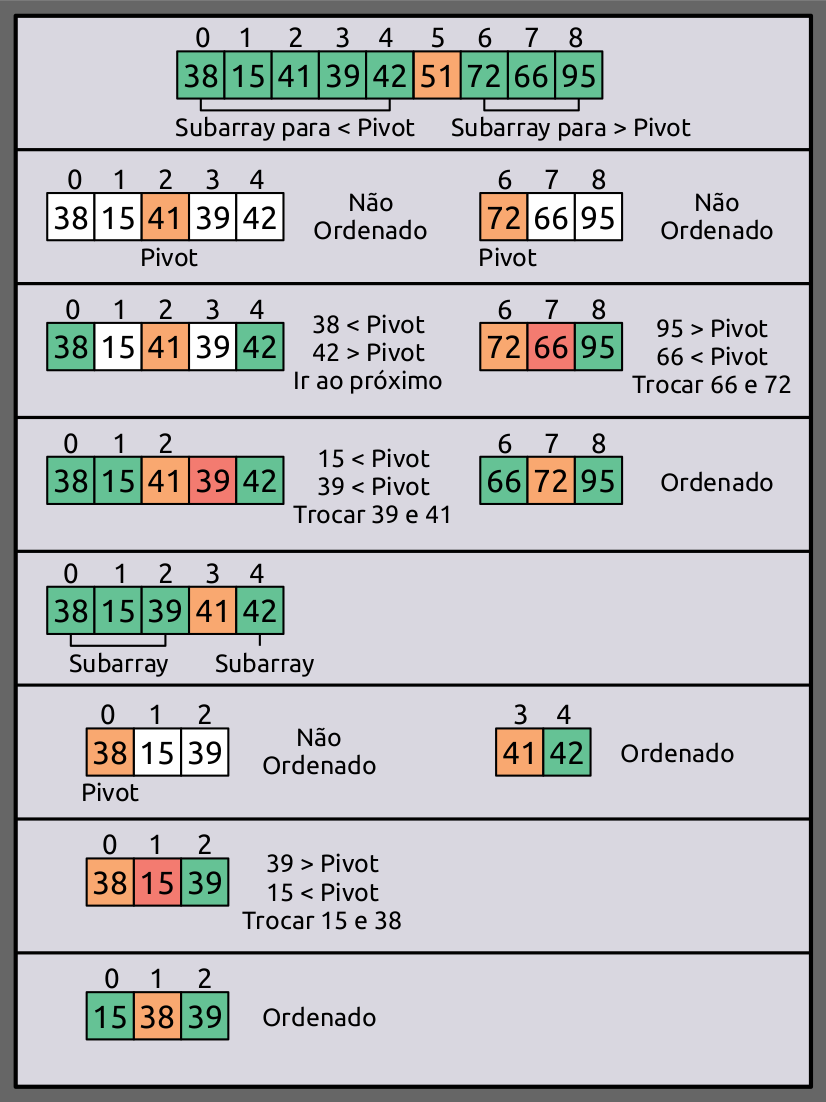
Por fim, obtemos o nosso array na forma ordenada:

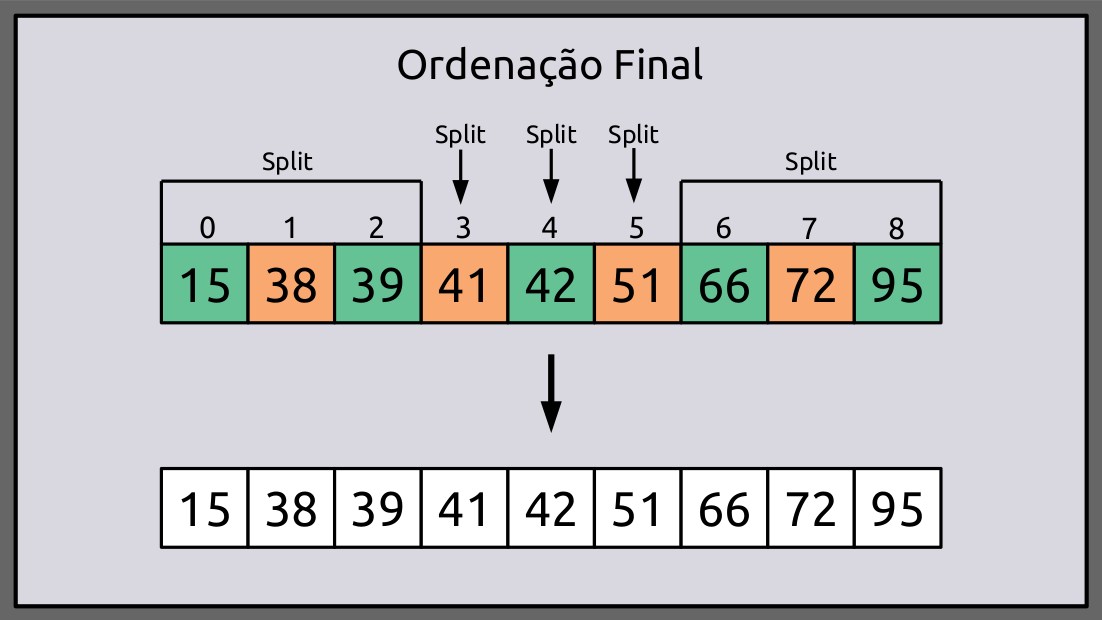
A versão in-place do Quick Sort tem uma complexidade de espaço de O(log n), mesmo na pior das hipóteses, quando é cuidadosamente implementada.

Que também se traduziria na seguinte receita:

1. Selecionar o valor do primeiro índice como pivot.
2. Marcar duas variáveis de ponteiro lower/left e upper/right.
3. Lower/Left será um ponteiro para os índices menores.
4. Upper/Right será um ponteiro para os índices maiores.
5. Enquanto o valor em Lower/Left for menor que o Pivot, mover para a direita.
6. Enquanto o valor em Upper/Right for maior que o Pivot, mover para a esquerda.
7. Se ambos os passos 5 e 6 não corresponderem, trocar Lower/Left e Upper/Right.
8. Se Lower/Left > Upper/Right, o ponto que eles se encontram é o novo pivot.

Vejamos agora essa versão implementada em Python:

def quick_sort(array):
	quick_sorter(array,0,len(array)-1)

def quick_sorter(array, first, last):
    if first < last:
        pivotindex = partition(array, first, last)
        quick_sorter(array, first, pivotindex - 1)
        quick_sorter(array, pivotindex + 1, last)
 
def partition(array, first, last):
    pivot = array[first]
    lower = first + 1
    upper = last
    done = False
    while not done:
        while lower <= upper and array[lower] <= pivot:
            lower += 1
        while array[upper] >= pivot and upper >= lower:
            upper -= 1
        if upper < lower:
            done = True
        else:
            temp = array[lower]
            array[lower] = array[upper]
            array[upper] = temp
    temp = array[first]
    array[first] = array[upper]
    array[upper] = temp
    return upper

lista = [6,1,22,355,13,77,99,444,30,7,80]
print(f'Lista Original: {lista}')
quick_sort(lista)
print(f'Lista Ordenada: {lista}')

Neste caso estamos utilizando uma função de partição que além de receber o array, também recebe o primeiro e o último elemento e eventualmente aplica as comparações e troca dos elementos.

Complexidade do Algoritmo Quick Sort

Complexidade Temporal

• Complexidade de Caso Pior (Big-O) O(n²): Ocorre quando o elemento pivot escolhido é sempre o maior ou menor do array.
• Complexidade de Caso Melhor (Big-Ômega) O(nlogn): Ocorre quando o elemento pivot é sempre o elemento do meio ou próximo ao elemento do meio.
• Complexidade de Médio Caso (Big-Theta) O(nlogn): Ele ocorre apenas quando as condições acimas não ocorrem.

Complexidade Espacial

A complexidade de espaço do algoritmo Quick Sort é O(logn) em grande partes das situações.

Conclusão

Através desse breve estudo foi possível compreendermos os fundamentos básicos sobre o algoritmo Quick Sort e como ele resolve o problema de ordenação de arrays.

Através de uma solução eficaz e elegante, que pode ser implementada com diversas variações que por sua vez podem impactar no seu desempenho em questão de complexidade de espaço e tempo, uma delas seria o Multi-Pivot Quick Sort, este que podemos considerar para estudos futuros.

Referências

• Quick Sort
• Data Structure and Algorithms - Quick Sort
• Quick Sort Algorithm
• Quick-Sort
• Quick Sort Tutorial
• Abdul Bari QuickSort Algorithm
• Quick Sort - Codeschool