Introdução
Merge Sort é um algoritmo de sorting/ordenação eficiente, de uso geral e baseado em comparação. A maioria das implementações produz uma ordenação estável, o que significa que a ordem dos elementos iguais é a mesma na entrada e na saída. O Merge Sort é um algoritmo de divisão e conquista que foi inventado por John von Neumann em 1945.
Dividir para Conquistar
Através da técnica de solução de problemas de Divisão e Conquista, nós dividimos um problema em subproblemas. Quando a solução de todos os subproblemas estiver concretizada, nós ‘unimos’ os resultados dos subproblemas de forma a resolver o problema principal.
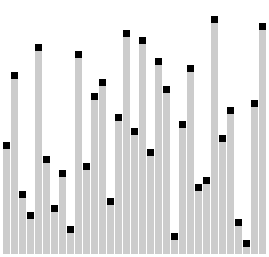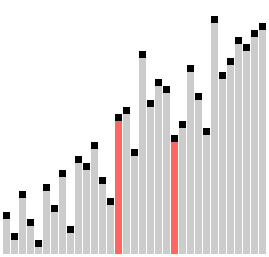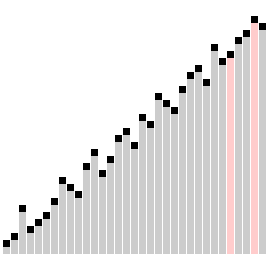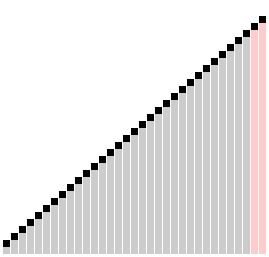
Considere que devemos ordenar um array X:
Um subproblema seria a ordenação de uma parte do array X, começando por um índice i e terminando em um índice j, denotados como X[i..j].
- Dividir
Se q é o ponto central entre i e j, então podemos dividir o array X[i..j] em dois arrays: X[i..q] e X[q+1..j].
- Conquistar
Na etapa de conquista, nós buscamos ordenar ambos os subarrays X[i..q] e X[q+1..j]. Caso ainda não tenhamos atingido o base case, nós novamente dividimos ambos os subarrays e tentamos novamente ordená-los.
- Combinar
Quando a etapa de conquista alcança o base case e nós obtemos dois arrays ordenados X[i..q] e X[q+1..j] para o array original X[i..j], nós combinamos os resultados, criando um array ordenado X[i..j] através dos dois arrays ordenados X[i..q] e X[q+1..j].
A figura a seguir visa ilustrar o procedimento do algoritmo Merge Sort:
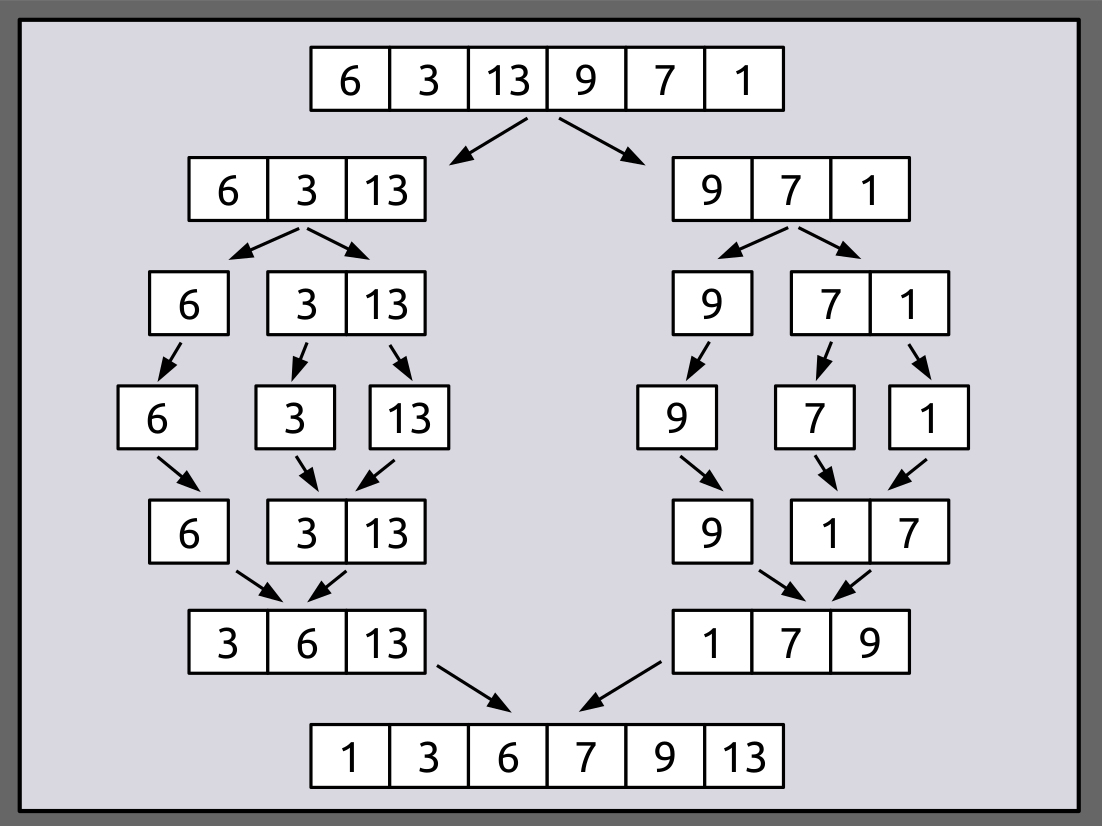
Procedimento
A função merge_sort() repetidamente divide o array em duas metades até que atinjamos um estágio onde tentamos executar a função merge_sort() em um subarray de tamanho 1, ou seja i == j.
Depois disso, a função merge() passará a atuar e combinará os arrays ordenados em arrays maiores até que o array inteiro esteja unido.
A Etapa Merge do Algoritmo Merge Sort
Como já sabemos, todo algoritmo recursivo é dependente de um base case e da habilidade de combinar resultados dos base cases. O algoritmo Merge Sort não é diferente: a etapa fundamental dele é a parte merge(união).
O algoritmo mantém três ponteiros, um ponteiro para cada um dos dois subarrays e um para manter o índice atual do array final(ordenado).
A ideia básica é fazermos a seguinte pergunta: Nós atingimos o fim de algum dos arrays?
-
Caso a resposta seja Não:
- Comparamos o elemento atual de ambos os arrays.
- Copiamos o elemento menor para o array ordenado.
- Movemos o ponteiro do array que contém o elemento menor.
-
Caso a resposta seja Sim:
- Copiamos todos elementos restantes do array não-vazio.
Para uma melhor compreensão do algoritmo, vamos considerar duas implementações diferentes em Python: uma versão Top-down(recursiva) e outra Bottom-up(iterativa).
Implementação em Python
Top-Down
A abordagem Top-Down é a metodologia que utiliza mecanismo de recursão. Começa no topo e prossegue para baixo.
Exemplo de código Python usando índices para o algoritmo Merge Sort Top-Down que divide recursivamente a lista em sublistas até o tamanho da sublista ser 1 e depois faz a união dessas sublistas para produzir uma lista ordenada.
def merge_sort(data):
"""
Função que determina se a lista está
dividida em partes individuais
"""
# Definimos o base case
if len(data) < 2:
return data
middle = len(data)//2
# Dividimos a lista em duas partes
left = merge_sort(data[:middle])
right = merge_sort(data[middle:])
# Unimos as duas partes ordenadas
merged = merge(left, right)
return merged
def merge(left, right):
"""
Quando os lados esquerdo/direito estiverem vazios,
Significa que é um item indiviual e está ordenado!
"""
# Garantimos que os lados esquerdo/direito não estão vazios,
# Indicando que é um item individual e já está ordenado
if not len(left):
return left
if not len(right):
return right
result = []
leftIndex = 0
rightIndex = 0
totalLen = len(left) + len(right)
while (len(result) < totalLen):
# Executamos as comparações necessários e unimos as duas partes
if left[leftIndex] < right[rightIndex]:
result.append(left[leftIndex])
leftIndex += 1
else:
result.append(right[rightIndex])
rightIndex += 1
if leftIndex == len(left) or rightIndex == len(right):
result.extend(left[leftIndex:] or right[rightIndex:])
break
return result
array = [6,3,13,9,7,1]
sorted_array = merge_sort(array)
print(sorted_array)Bottom-Up
A abordagem Bottom-Up usa metodologia iterativa. Começa com um array de “elemento único” e combina dois elementos adjacentes e também ordena ambos ao mesmo tempo.
Os arrays ordenados combinados são novamente combinados e ordenados entre si até que uma única unidade do array ordenado seja atingida, então teremos o problema solucionado.
Exemplo de código Python usando índices para o algoritmo Merge Sort Bottom-Up, que trata a lista como um array de n sublistas de tamanho 1 e mescla iterativamente as sublistas entre dois buffers:
def merge_sort(lst):
if not lst:
return []
lists = [[x] for x in lst]
while len(lists) > 1:
lists = merge_lists(lists)
return lists[0]
def merge_lists(lists):
result = []
for i in range(0, len(lists) // 2):
result.append(merge(lists[i*2], lists[i*2 + 1]))
if len(lists) % 2:
result.append(lists[-1])
return result
def merge(xs, ys):
i = 0
j = 0
result = []
while i < len(xs) and j < len(ys):
x = xs[i]
y = ys[j]
if x > y:
result.append(y)
j += 1
else:
result.append(x)
i += 1
result.extend(xs[i:])
result.extend(ys[j:])
return result
array = [10,2,4,5,9,66,300,13]
sorted_array = merge_sort(array)
print(sorted_array)Complexidade do Algoritmo Merge Sort
Complexidade Temporal
- Complexidade de Caso Pior (Big-O):
O(nlogn) - Complexidade de Caso Melhor (Big-Ômega):
O(nlogn): típico ouO(n): variante natural - Complexidade de Médio Caso (Big-Theta):
O(nlogn)
Complexidade Espacial
- Complexidade de Caso Pior:
O(n)
Conclusão
Através desse breve estudo foi possível compreendermos a importância e relevância do algoritmo Merge Sort na Ciência da Computação, especialmente por ter sido desenvolvido por um dos pais da Computação: John Von Neumann e por sua alta eficiência na solução do problema de ordenação.
Existem diversas variações do algoritmo Merge Sort que podem impactar diretamente em sua complexidade, para adquirir mais conhecimento sobre este algoritmo, selecionamos importantes referências para você se aprofundar.