Introdução
Insertion Sort é um algoritmo de ordenação simples que cria o array(ou lista) final ordenando um item por vez. É muito menos eficiente em listas grandes do que algoritmos mais avançados, como Quick Sort, Heap Sort ou Merge Sort. No entanto, a Ordenação por Inserção oferece várias vantagens:
- Eficiente para conjuntos de dados pequenos, como outros algoritmos de ordenação quadrática
- Mais eficiente na prática do que a maioria dos outros algoritmos quadráticos simples (ou seja,
O(n²)), como Selection Sort ou Bubble Sort - Adaptável, isto é, eficiente para conjuntos de dados que já estão substancialmente ordenados: a complexidade do tempo é
O(kn)quando cada elemento do input está a não mais de k locais da sua posição ordenada - Estável, ou seja, não altera a ordem relativa dos elementos com chaves iguais
- In-Place, ou seja, requer apenas uma quantidade constante
O(1)de espaço de memória adicional
Quando as pessoas ordenam manualmente as cartas de um deck em uma mão, a maioria usa um método semelhante ao Insertion Sort.
Algoritmo
Para ordenar um array de tamanho n em ordem crescente:
- Itere de
array[1]paraarray[n]no array em questão. - Compare o elemento atual (chave) com seu predecessor.
- Se o elemento-chave for menor do que seu predecessor, compare-o com os elementos anteriores. Mova os elementos maiores uma posição para cima para liberar espaço para o elemento trocado.
Por exemplo:
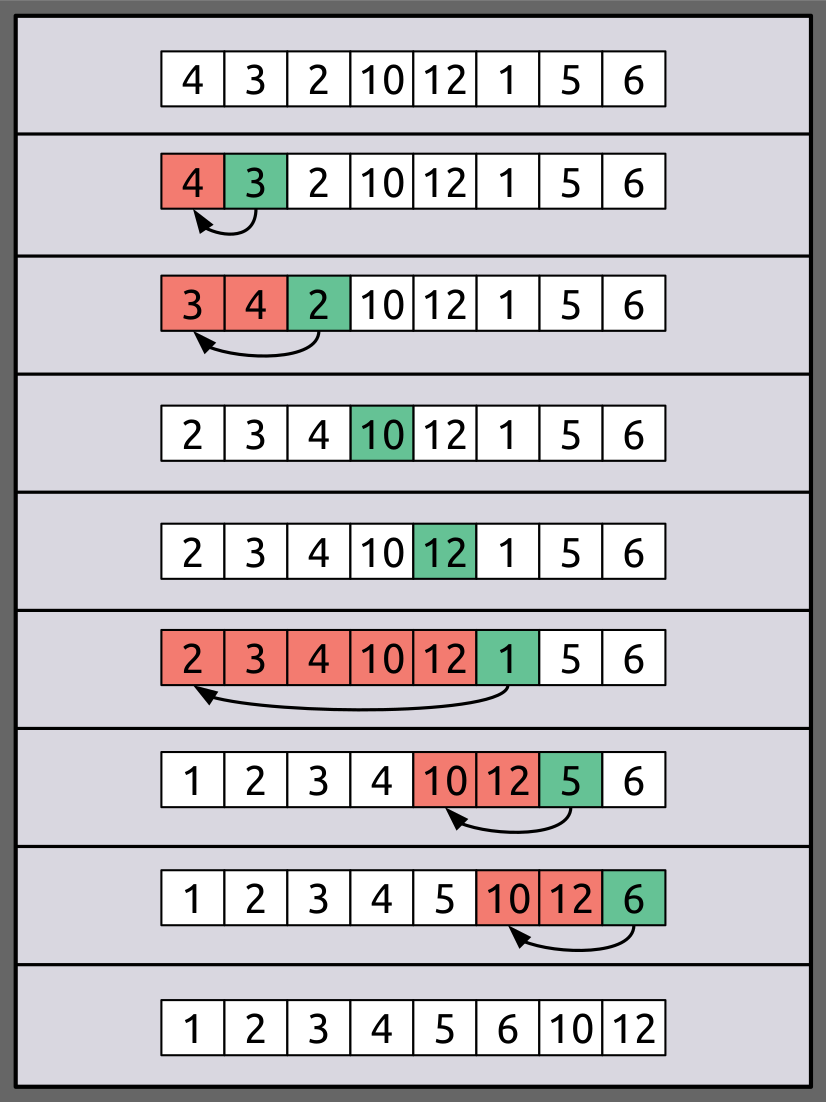
Procedimento
- O primeiro passo envolve a comparação do elemento em questão com seu elemento adjacente.
- Se a cada comparação for revelado que o elemento em questão pode ser inserido em uma posição específica, é criado espaço para ele deslocando os outros elementos uma posição para a direita e inserindo o elemento na posição adequada.
- O procedimento acima é repetido até que todos os elementos no array estejam na posição apropriada.
A figura a seguir ilustra o procedimento detalhado do Algoritmo Insertion Sort:
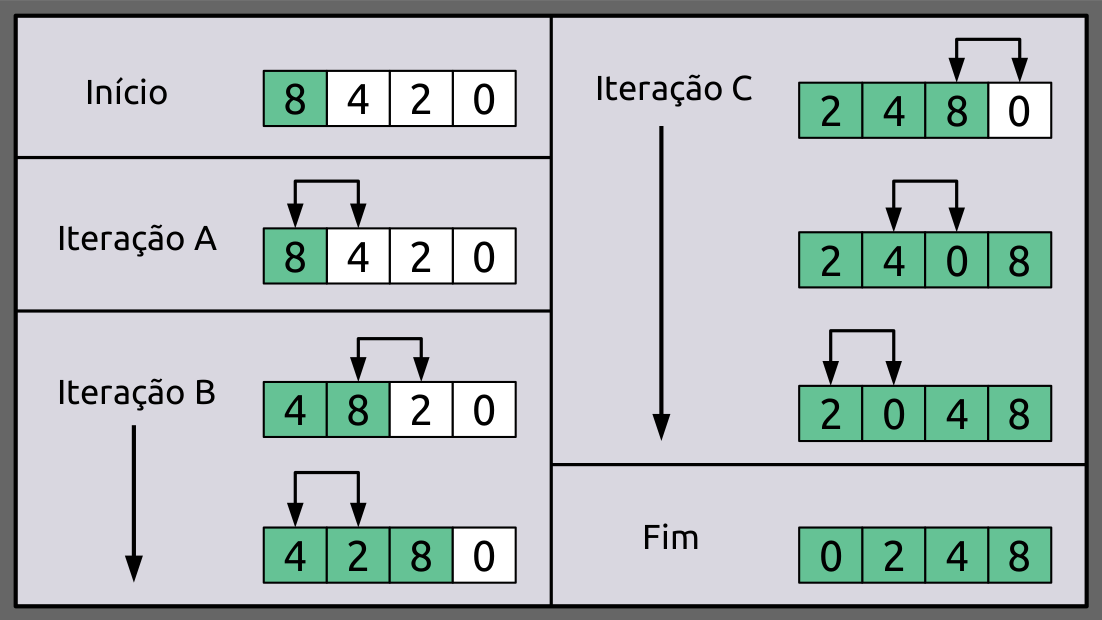
Estamos considerando o array: [8,4,2,0]
- Iteração A: Comparamos 8 com 4. A comparação mostra que
4 < 8, então fazemos a troca dos elementos.
O array agora se encontra como: [4,8,2,0]
- Iteração B: Inicia com o segundo elemento 8, porém ele já foi trocado e está na posição correta, então movemos para o próximo elemento. Agora estamos no terceiro elemento de valor 2, e iremos compará-lo com os elementos que precedem ele.
Comparamos 8 com 2. A comparação mostra que 2 < 8, então fazemos a troca dos elementos. Novamente comparamos 4 com 2 e a comparação mostra que 2 < 4, então fazemos a troca dos elementos.
O array agora se encontra como: [2,4,8,0]
- Iteração C: Inicia com o terceiro elemento 8, porém ele já foi trocado e está na posição correta, então movemos para o próximo elemento. Agora estamos no quarto elemento de valor 0 e iremos compará-lo com os elementos que precedem ele.
Comparamos 8 com 0. A comparação mostra que 0 < 8, então fazemos a troca dos elementos. Novamente comparamos 4 com 0 e a comparação mostra que 0 < 4, então fazemos a troca dos elementos, por fim, comparamos 2 com 0 e temos que 0 < 2, então é feita a última troca.
Finalmente o array se encontra ordenado: [0,2,4,8]
Implementação em Python
A seguir temos a implementação do Algoritmo Insertion Sort em Python:
def swap(array, i, j):
if i != j:
array[i], array[j] = array[j], array[i]
def insertionsort(array):
for i in range(1, len(array)):
j = i
while j > 0 and array[j - 1] > array[j]:
swap(array, j, j - 1)
j -= 1
return array
array = [3,4,5,6,1,2]
sorted_array = insertionsort(array)
print(sorted_array) # [1, 2, 3, 4, 5, 6]Observe que definimos uma função helper chamada de swap() que será responsável por trocar a posição dos elementos.
Animação com Matplotlib
A biblioteca matplotlib nos permite criar gráficos de diversos formatos e até mesmo construir animações.
No código a seguir, transformamos o Algoritmo Insertion Sort em um generator através da palavra-chave yield, de forma que consigamos acessar cada etapa do algoritmo.
import matplotlib.animation as animation
import matplotlib.pyplot as plt
import random
def swap(array, i, j):
if i != j:
array[i], array[j] = array[j], array[i]
def insertionsort(array):
for i in range(1, len(array)):
j = i
while j > 0 and array[j - 1] > array[j]:
swap(array, j, j - 1)
j -= 1
yield array
N = 40
array = [x + 1 for x in range(N)]
random.shuffle(array)
generator = insertionsort(array)
writergif = animation.PillowWriter(fps=30)
fig, ax = plt.subplots()
plt.grid()
bar_rects = ax.bar(range(len(array)), array, align="edge", color='k')
ax.set_xlim(0, N)
ax.set_ylim(0, int(1.07 * N))
text = ax.text(0.02, 0.95, "", transform=ax.transAxes)
iteration = [0]
def update_fig(array, rects, iteration):
for rect, val in zip(rects, array):
rect.set_height(val)
iteration[0] += 1
text.set_text(f"N of operations: {iteration[0]}")
anim = animation.FuncAnimation(fig, func=update_fig,
fargs=(bar_rects, iteration), frames=generator, interval=1,
repeat=False, save_count=400)
anim.save('insertion.gif', writer=writergif)A variável N guarda o número de itens do array que iremos ordenar, a variável array constrói nosso array que em seguida é embaralhado com o método shuffle() e usado como input para o algoritmo Insertion Sort, que nos retorna um gerador.
Em seguida, definimos a figura onde o gráfico será desenhado e construímos os retângulos do gráfico com a variável bar_rects.
A função update_fig() é responsável por atualizar a figura e o número de iterações ocorrentes.
O método animation.FuncAnimation() cria a animação ao chamar repetidamente a função update_fig()
Finalmente, salvamos a figura como insertion.gif com o auxílio do writer PillowWriter, que nos traz o seguinte resultado:
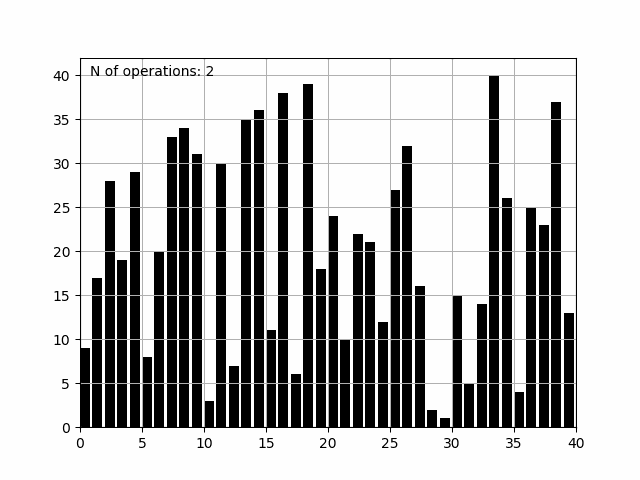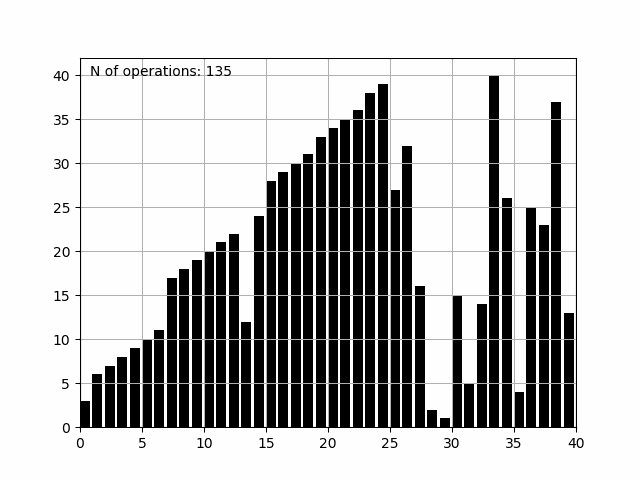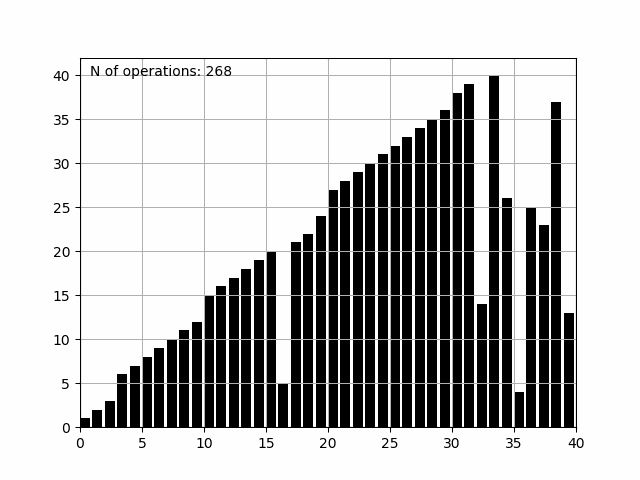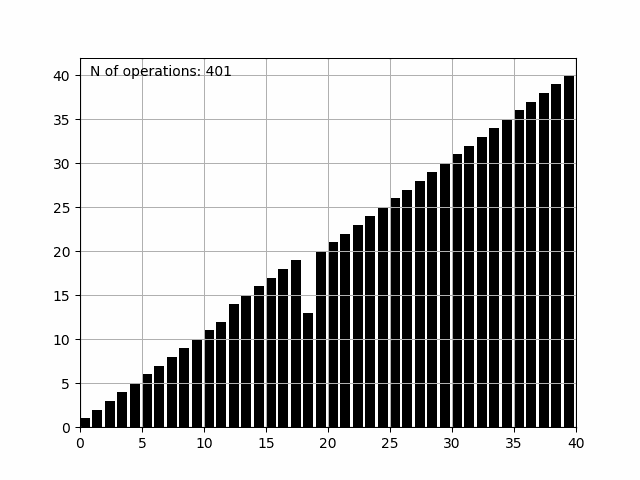
Complexidade do Algoritmo Insertion Sort
Complexidade Temporal
- Complexidade de Caso Pior (Big-O): O input de pior caso é um array ordenado em ordem inversa. O conjunto de todas as entradas do pior caso consiste em todos os arrays em que cada elemento é o menor ou o segundo menor dos elementos anteriores a ele. Nesses casos, toda iteração do loop interno varrerá e mudará toda a subseção ordenada da matriz antes de inserir o próximo elemento. Isso fornece à ordenação por inserção um tempo de execução quadrático
O(n²). - Complexidade de Caso Melhor (Big-Ômega): O melhor caso de input é um array que já está ordenado. Nesse caso, o Insertion Sort tem um tempo de execução linear
O(n). Durante cada iteração, o primeiro elemento restante da entrada é comparado apenas com o elemento mais à direita da subseção ordenada do array. - Complexidade de Médio Caso (Big-Theta): O caso médio também é quadrático,
O(n²), o que torna o Insertion Sort impraticável para ordenar grandes arrays. No entanto, o Insertion Sort é um dos algoritmos mais rápidos para ordenar arrays muito pequenas, ainda mais rápido que o Quick Sort, de fato, boas implementações de Quick Sort usam Insertion Sort para arrays menores que um determinado limite.
Complexidade Espacial
A complexidade do espaço é O(1) porque uma chave variável extra é usada.
Conclusão
Através deste breve estudo foi possível compreendermos o funcionamento e uso do Algoritmo Insertion Sort, bem como, implementá-lo na linguagem Python.
Embora ele não seja um algoritmo considerado eficiente, existem casos de usos em que ele pode ser eficaz, especialmente quando estamos lidando com arrays de poucos elementos.