Introdução
Heap Sort é um algoritmo de sorting, baseado em comparação.
O Heap Sort pode ser imaginado como a versão do algoritmo Selection Sort aprimorada: Como o selection sort, o Heap Sort divide o input em uma região ordenada e uma região não-ordenada, e reduz iterativamente a região não-ordenada, extraindo o elemento maior e inserindo-o na região ordenada.
Diferente do selection sort, o Heap Sort não perde tempo com uma verificação de tempo linear da região não-ordenada; em vez disso, ele mantém a região não-ordenada em uma estrutura de dados de heap para encontrar mais rapidamente o maior elemento em cada etapa.
Heap Sort foi inventado por J. W. J. Williams em 1964, ano que também foi o nascimento do heap, apresentado por Williams como uma estrutura de dados útil.
Heap
Heap é uma estrutura de dados árvore que satisfaz as seguintes propriedades:
- Propriedade de Forma: Heap é sempre uma árvore binária completa, o que significa que todos os níveis de uma árvore estão totalmente preenchidos. Não deve haver um nó que tenha apenas um filho. Todos os nós, exceto folhas, devem ter dois filhos; apenas um heap é chamado como uma árvore binária completa.
- Propriedade da Heap: Todos os nós - são maiores ou iguais a - ou - menores ou iguais a - cada um de seus filhos. Isso significa que se o nó pai for maior que o nó filho, ele será chamado como um max heap. Considerando que, se o nó pai for menor que o nó filho, ele será chamado como um min heap.
Procedimento
Existem basicamente duas fases envolvidas na ordenação dos elementos usando o algoritmo Heap Sort:
- Primeiramente, inicia-se com a construção da Heap ao ajustar os elementos do array.
- Uma vez que a Heap está criada: Elimine repetidamente o elemento raiz(root) do Heap deslocando-o para o final do array e, em seguida, armazene a estrutura do heap com os elementos restantes.
Considere um array de N elemento distintos em memória, o algoritmo Heap Sort então trabalhará da seguinte maneira:
- Inicialmente, a Heap é construída ao mover os elementos para suas posições apropriadas no array. Isso significa que, à medida que os elementos são percorridos no array, a raiz, seu filho esquerdo e seu filho direito são preenchidos, respectivamente, formando uma árvore binária.
- Na segunda fase o elemento raiz é eliminado da Heap, sendo assim, movido para o fim do array.
- Os elementos que ficaram, podem não ser uma Heap, sendo assim, repetimos os passos
1e2para que tenhamos uma Max-Heap. Os procedimentos se repetem até que tenhamos todos os elementos eliminados, assim teremos nosso array ordenado.
É importante frisar que ao eliminar um elemento da Heap, é necessário decrementar o valor do índice do array em 1. Os elementos são eliminados em ordem decrescente para um max heap e em ordem crescente para min heap.
Exemplo
No diagrama abaixo, inicialmente há um Array não-ordenado com 6 elementos e, em seguida, o max heap será construído:
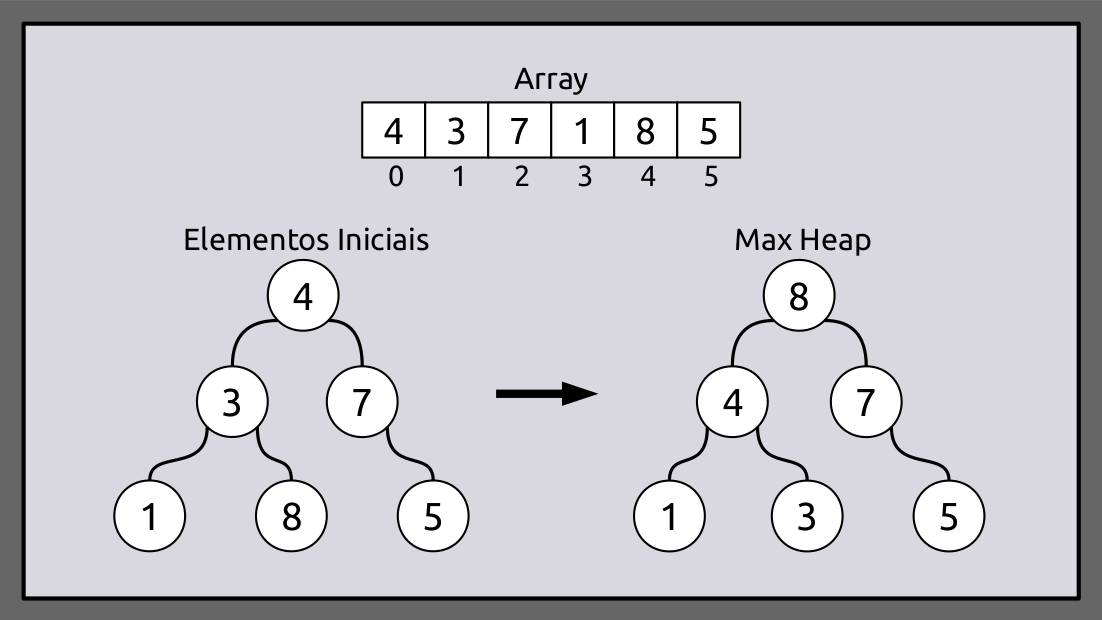
Após construir o max heap, os elementos no array serão:
Array = [8, 4, 7, 1, 3, 5]E então as seguintes etapas são executadas:
- Etapa 1: 8 é trocado por 5.
- Etapa 2: 8 é desconectado da heap, pois 8 está na posição correta.
- Etapa 3: O max heap é criado e 7 é trocado por 3.
- Etapa 4: 7 é desconectado do heap.
- Etapa 5: O max heap é criado e 5 é trocado por 1.
- Etapa 6: 5 é desconectado do heap.
- Etapa 7: O max heap é criado e 4 é trocado por 3.
- Etapa 8: 4 é desconectado do heap.
- Etapa 9: O max heap é criado e 3 é trocado por 1.
- Etapa 10: 3 é desconectado.
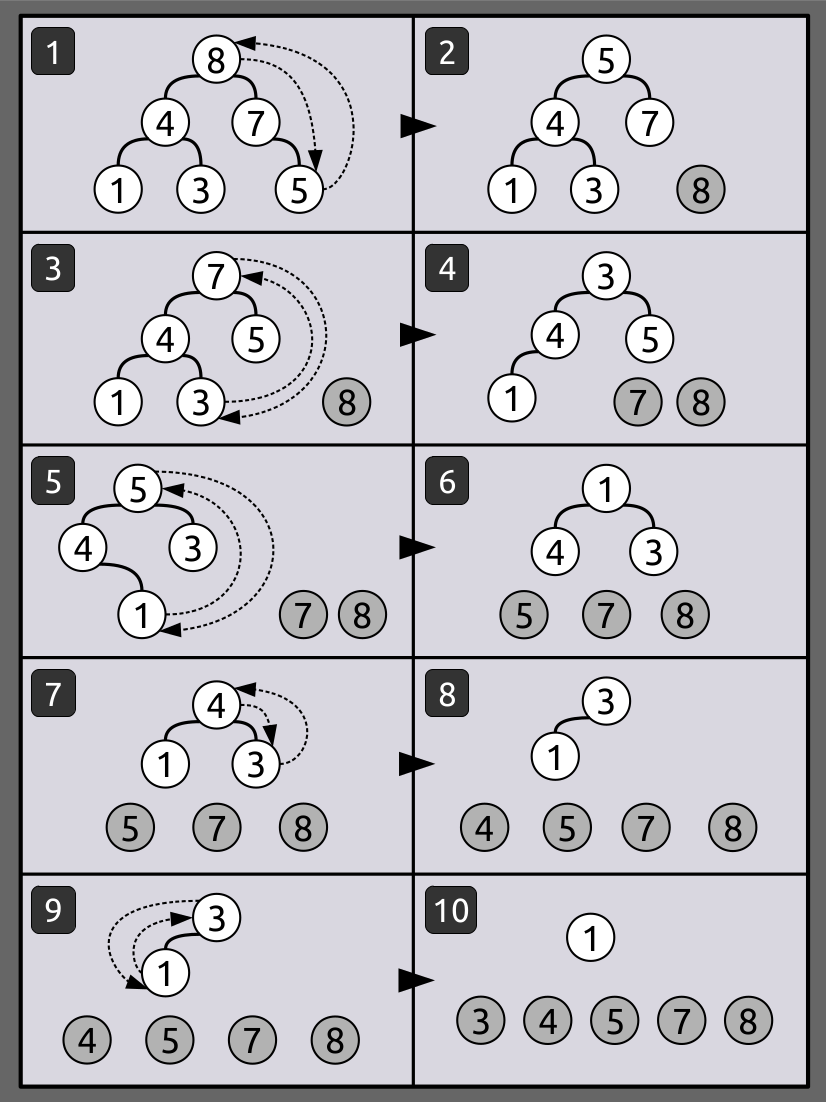
Depois de executar todas as etapas, teremos o Array ordenado:
Array = [1, 3, 4, 5, 7, 8]Vejamos agora como podemos implementar este algoritmo com a linguagem Python.
Implementação em Python
A seguinte implementação constrói uma Max-Heap através da função heapify():
def heapify(array, n, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
# Verifica se o filho a esquerda da raiz existe
# e se ele é maior do que a raiz
if (left < n and array[i] < array[left]):
largest = left
# Verifica se o filho a direita da raiz existe
# e se ele é maior do que a raiz
if (right < n and array[largest] < array[right]):
largest = right
# Altera a raíz se necessário
if (largest != i):
# faz o swap
array[i],array[largest] = array[largest],array[i]
heapify(array, n, largest)
def heap_sort(array):
n = len(array)
# Constrói a Heap
for i in range(n, -1, -1):
heapify(array, n, i)
# Extrai os elementos um por um
for i in range(n-1, 0, -1):
# faz o swap
array[i], array[0] = array[0], array[i]
heapify(array, i, 0)
return array
array = [4,3,7,1,8,5]
array_ordenado = heap_sort(array)
print(array_ordenado)Complexidade do Algoritmo Heap Sort
Complexidade Temporal
- Complexidade de Caso Pior (Big-O):
O(nlogn) - Complexidade de Caso Melhor (Big-Ômega):
O(nlogn) - Complexidade de Médio Caso (Big-Theta):
O(nlogn)
Complexidade Espacial
O algoritmo Heap Sort tem uma complexidade espacial constante O(1)
Conclusão
O algoritmo de Heap Sort é uma técnica de sorting/ordenação que se utiliza da estruturas de dados árvores binárias Heap.
Como sabemos que os Heaps sempre devem seguir uma ordem específica, podemos aproveitar essa propriedade e usá-la para encontrar o elemento de valor máximo e ordenar sequencialmente elementos selecionando o nó raiz de um Heap e adicionando-o ao final do array.
Com o estudo do algoritmo Heap Sort fomos capazes de reconhecer a importância da combinação de estruturas de dados com procedimentos - nesse caso específico implementado - utilizamos uma árvore binária Max-Heap para resolver o problema de ordenação de um array em um tempo considerável.