"Computer Science is no more about computers than astronomy is about telescopes."
Introdução
O algoritmo de Dijkstra é um algoritmo para encontrar os caminhos mais curtos entre vértices em um grafo, que pode representar, por exemplo, redes rodoviárias. Foi concebido pelo cientista da computação Edsger Wybe Dijkstra em 1956 e publicado três anos depois.
Para um determinado vértice de origem no grafo, o algoritmo encontra o caminho mais curto entre esse vértice e todos os outros. Também pode ser usado para encontrar os caminhos mais curtos de um único vértice de origem para um único vértice de destino, parando o algoritmo uma vez que o caminho mais curto para o vértice de destino foi determinado.
O campo da ciência da computação abrange uma ampla variedade de problemas. O problema do caminho mais curto é importante, e vemos muitas aplicações dele diariamente.
Por exemplo, muitas vezes precisamos encontrar o caminho mais curto entre dois pontos durante a viagem. Aplicativos de mapeamento da Web, como o Google Maps, usam esses algoritmos para exibir as rotas mais curtas.
O problema do caminho mais curto pode ser resolvido usando diferentes algoritmos, como Breadth-First Search (BFS) ou algoritmo Floyd-Warshall. No entanto, o algoritmo de caminho mais curto mais popular e ideal é o algoritmo de Dijkstra.
Representação do Problema
Problemas de caminho mais curto são representados na forma de um grafo. Antes de prosseguir, vamos rever nosso conhecimento sobre conceitos de grafos.
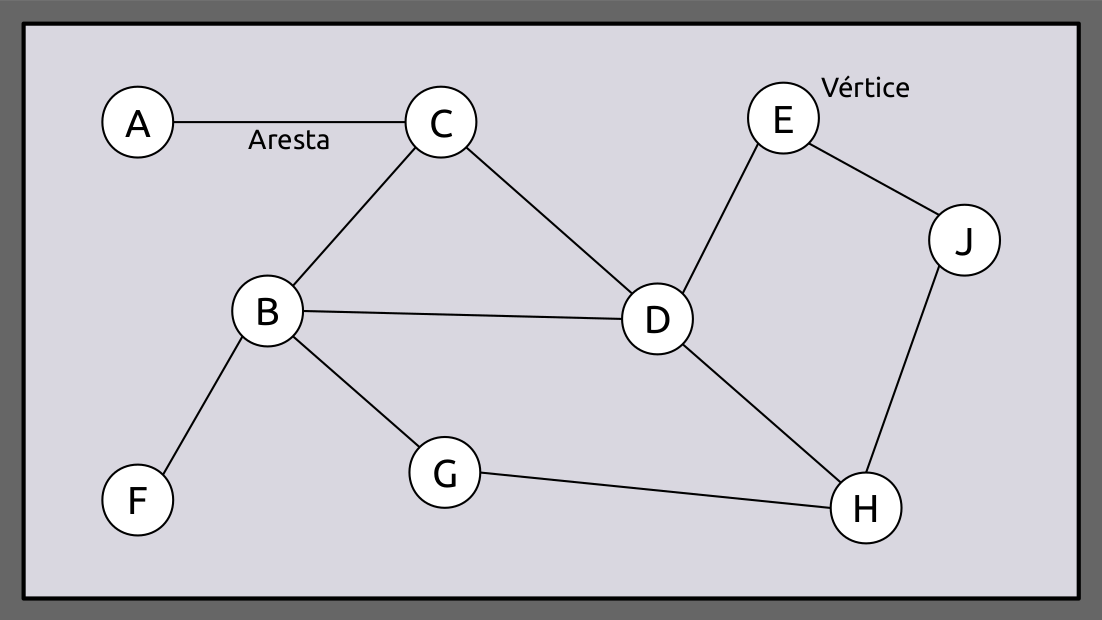
Para problemas de caminho mais curto, os vértices representam cidades (ou pontos) e as arestas representam a conectividade, ou conexão, de um vértice a outro, conforme ilustrado abaixo. Esses tipos de problemas podem ter um ou mais vértices de origem a partir dos quais os caminhos são determinados. Este problema pode ser representado usando grafos direcionados ou não-direcionados.
O Algoritmo
Agora que estabelecemos a representação do problema, vamos discutir o algoritmo de Dijkstra. Ele requer que o grafo de entrada tenha apenas um vértice de origem. Também requer que todas as arestas do grafo tenham pesos não-negativos.
Suponha que recebemos um mapa como o abaixo e desejamos viajar da cidade A para a cidade F. Em um grafo simples como este, podemos ver que existem vários caminhos para viajar de A a F.
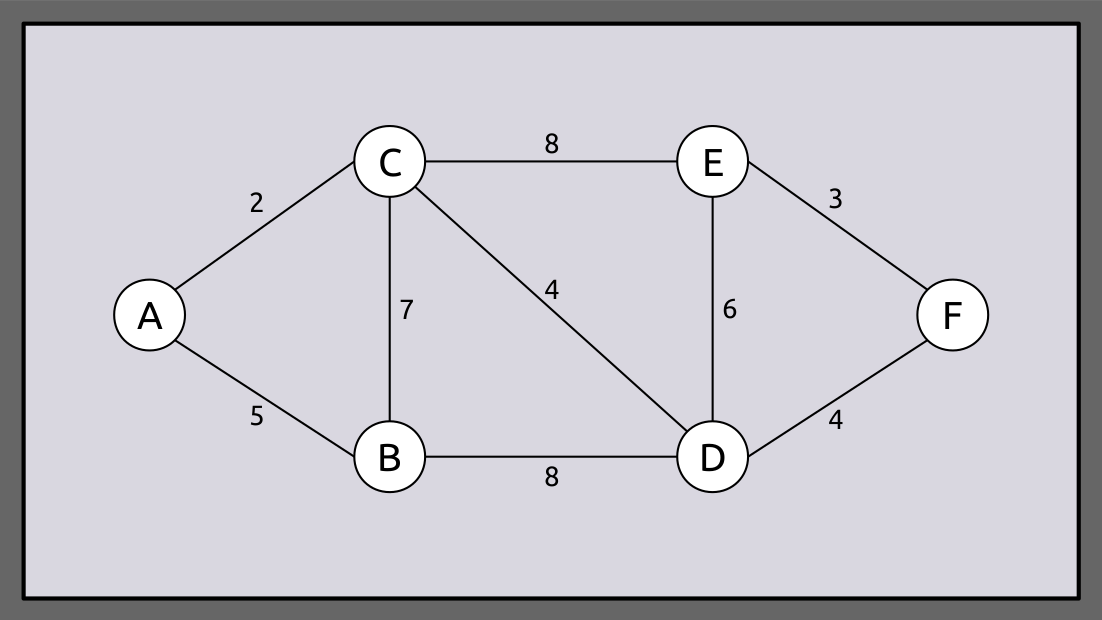
Depois de uma boa olhada, você perceberá que o caminho A → C → D → F nos dará o caminho mais curto. Mas isso exige muito pensamento, e você provavelmente teve que analisar cada caminho um por um antes de chegar à conclusão.
Mas e se você tiver um grafo mais complicado com centenas de cidades? Nesse caso, você pode usar o algoritmo de Dijkstra. Isso facilita esse trabalho encontrando os valores de distância do caminho para cada vértice não-visitado v. Este valor de distância será a distância mais curta desse vértice v do vértice de origem. Isso ajuda a determinar o caminho mais curto.
Vamos mergulhar fundo no algoritmo inicializando algumas variáveis que são necessárias para o algoritmo de Dijkstra. Vamos precisar do seguinte:
- Uma lista de todos os vértices não-visitados no grafo.
- Uma lista de distâncias com seus vértices no grafo. Inicialmente, a distância de todos os vértices é inicializada como infinito, exceto o vértice de origem (que é inicializado como 0).
- Uma lista de todos os vértices que são visitados e que fazem o caminho mais curto. A princípio, essa lista conterá apenas o vértice de origem.
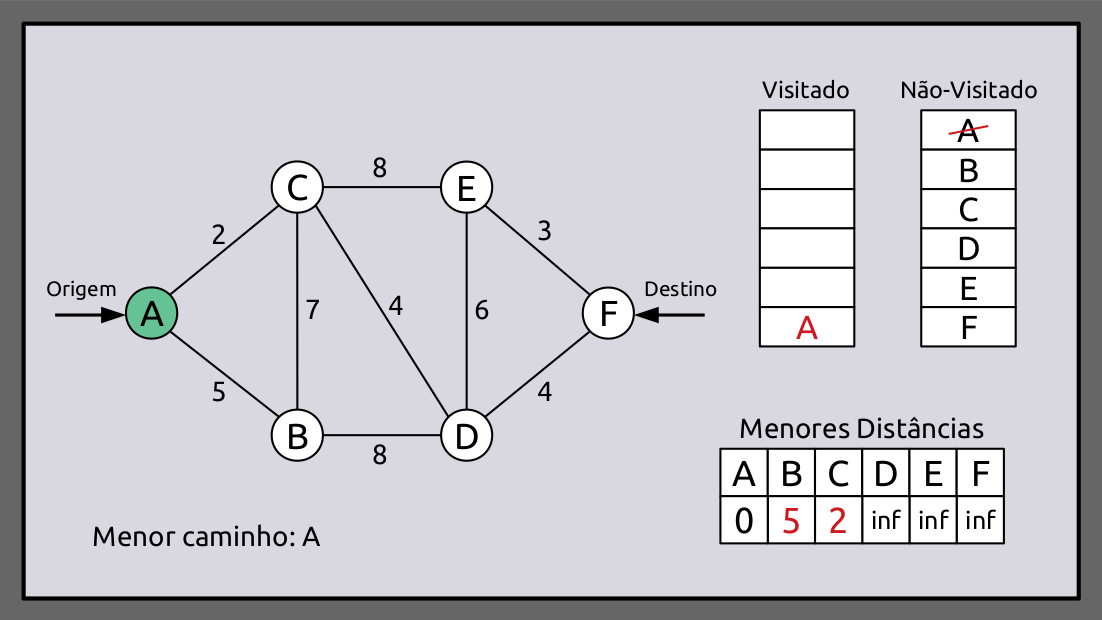
O algoritmo começa a partir do vértice de origem, que neste caso é A. Mudamos as distâncias dos vértices B e C na lista de distâncias para 5 e 2. Como a soma do valor da distância do vértice de origem aos vértices B e C é maior do que a distância original, eles são alterados. O grafo e as listas correspondentes têm a aparência ilustrada abaixo.
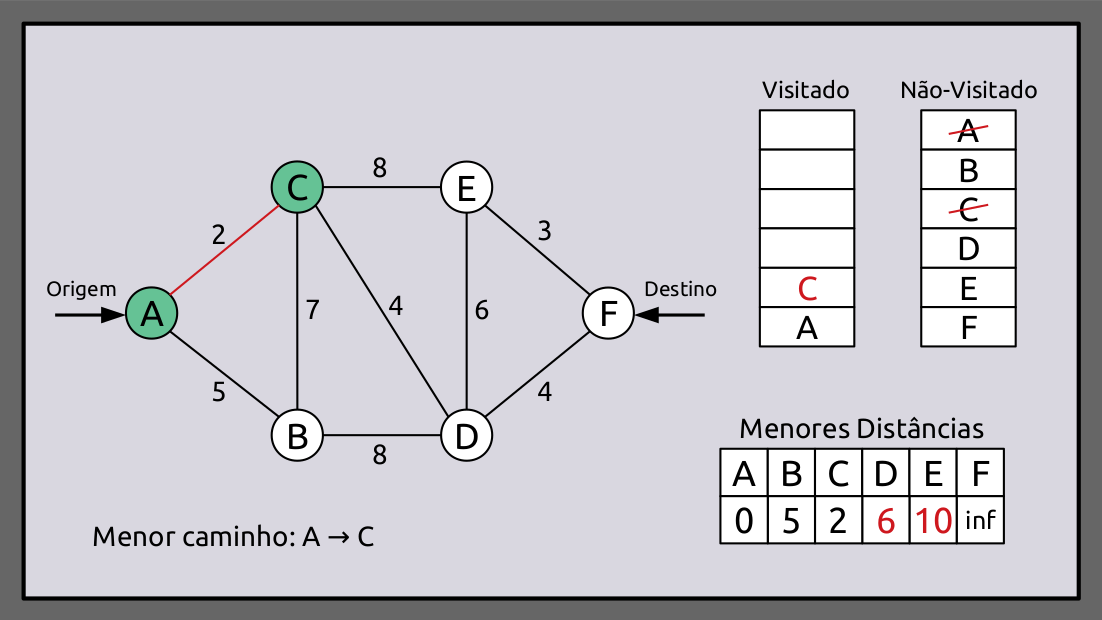
Agora nos movemos em direção ao vértice não-visitado com a menor distância, que é o vértice C. As distâncias dos vértices D e E agora são atualizadas para 6 e 10.
Como a soma da distância do vértice origem aos vértices D e E é maior que a distância original, isso foi atualizado.
No caso do vértice D, a distância de A a C é 2 e C a D é 4. Assim, a distância total do vértice de origem A para D tornou-se 2 + 4 = 6.
O vértice E foi atualizado da mesma maneira. Como C fornece o caminho mais curto até agora, ele é adicionado ao caminho mais curto. As alterações são implementadas conforme ilustrado abaixo.
O vértice não-visitado com o menor valor de distância agora é B. Como visitar B não abre nenhum novo caminho, os valores de distância dos vértices permanecem inalterados e também não são adicionados ao caminho. B agora é movido para a lista de vértices visitados.
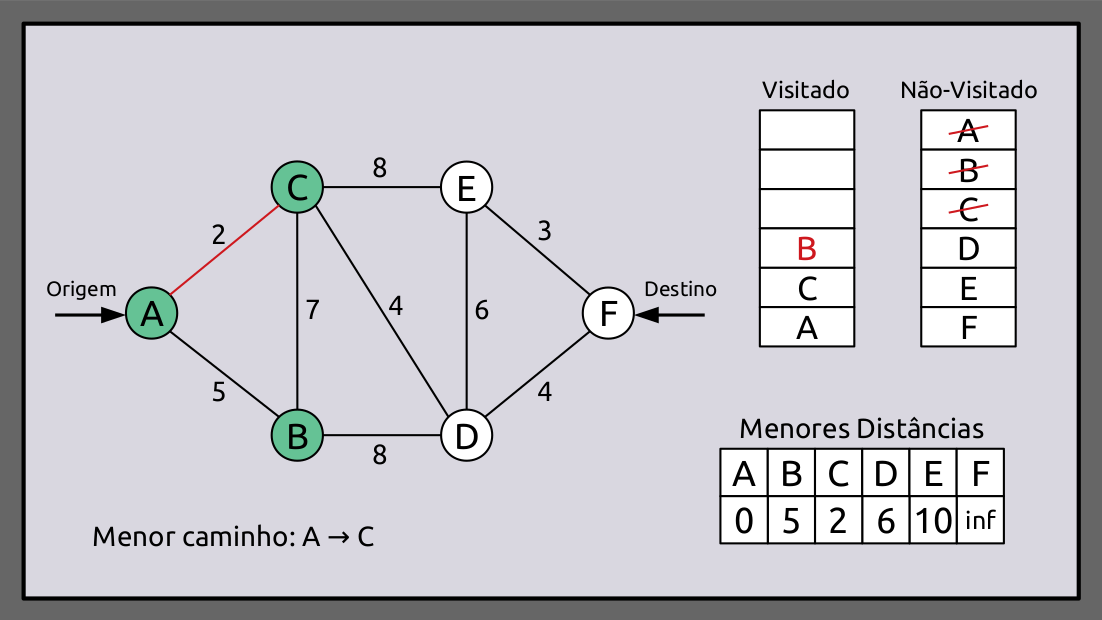
Agora, D é o vértice não-visitado com o menor valor de distância. Ao visitar o vértice D, encontramos uma nova conexão F e atualizamos seu valor de distância para 2 + 4 + 4 = 10. Isso é adicionado ao caminho mais curto, pois o vértice D fornece o caminho mais curto que o vértice anterior C.
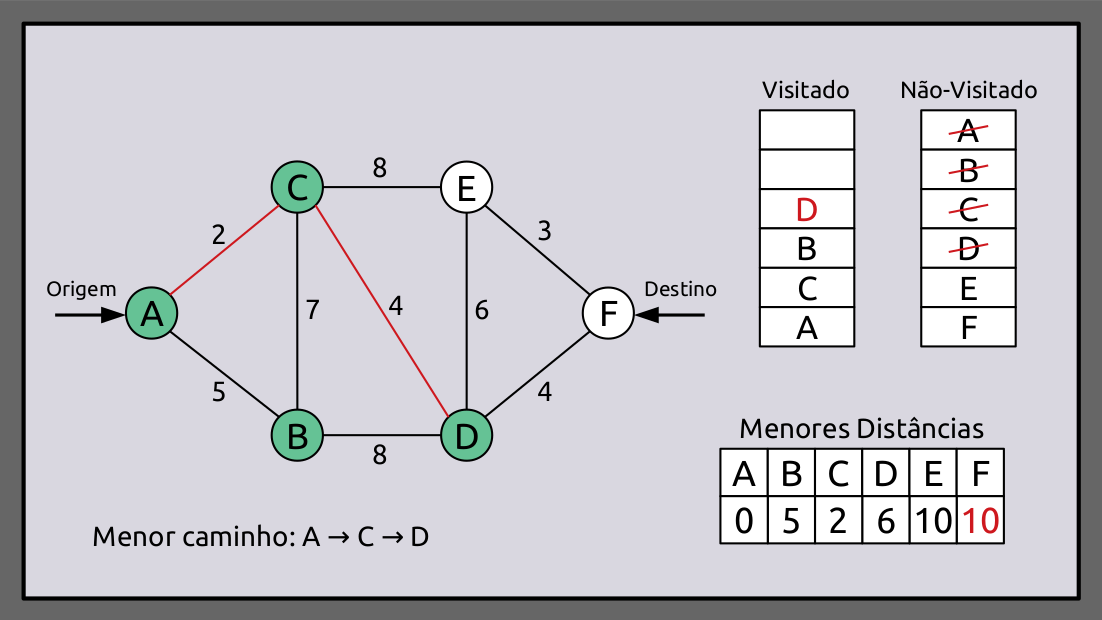
Agora os vértices E e F têm valores de distância semelhantes. Prosseguindo em ordem lexicográfica, visitaremos primeiro o vértice E. Isso não adiciona ao caminho mais curto e também não altera os valores de distância dos vértices.
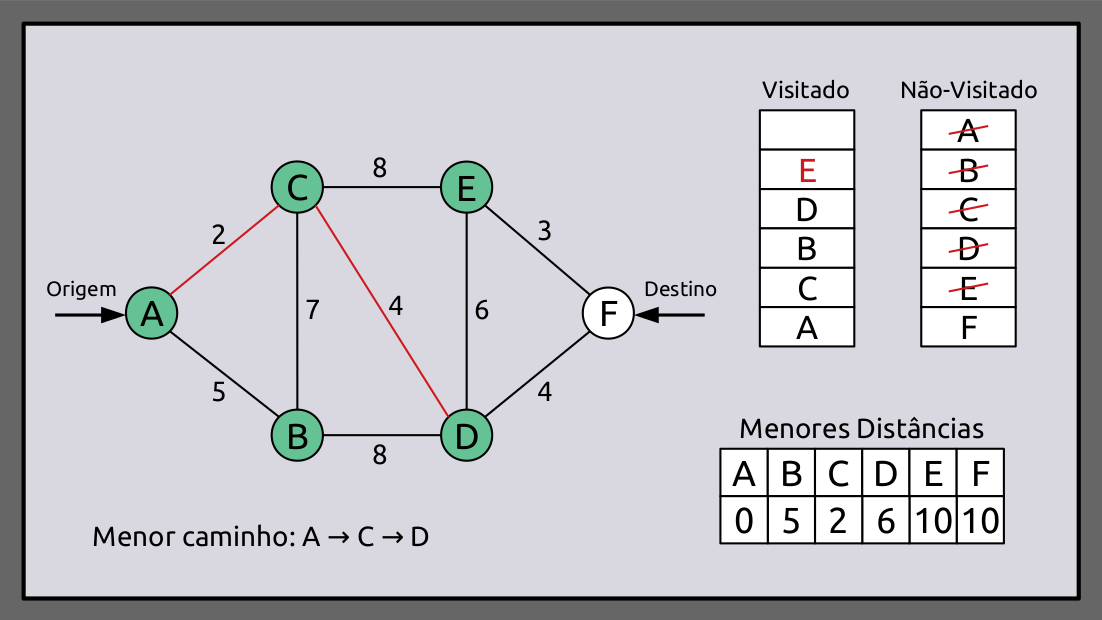
O último vértice a visitar é F, que também é nosso vértice de destino. O caminho mais curto agora é concluído adicionando o caminho do vértice D a F. O peso total desse caminho mais curto é 10. Todos os outros caminhos que levam ao vértice de destino F darão uma distância maior que 10.
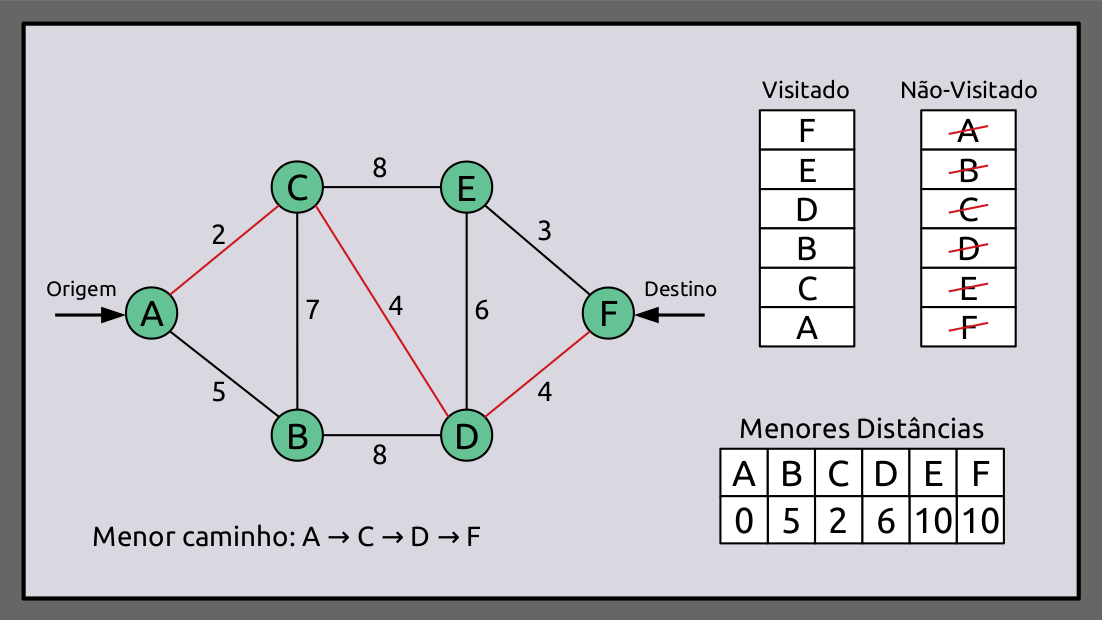
Agora que vimos um exemplo ilustrativo, vamos pensar um pouco mais sobre o algoritmo na prática, para isso, utilizaremos a linguagem Python.
Implementação
Primeiramente vamos definir uma tupla que irá conter cada um dos vértices:
nodes = ('A', 'B', 'C', 'D', 'E', 'F')Também iremos definir um dicionário que armazenará as distâncias de cada vértice:
distances = {
'A': {'C': 2, 'B': 5},
'B': {'A': 5, 'D': 8, 'C': 7},
'C': {'A': 2, 'E': 8, 'D': 4, 'B': 7},
'D': {'B': 8, 'C': 4, 'E': 6, 'F': 4},
'E': {'F': 3, 'D': 6, 'C': 8},
'F': {'D': 4, 'E': 3}
}A seguir, construímos um método que será responsável por computar os vértices pais e também cada vértice visitado e sua respectiva somatória de pesos:
def find_route(current, end):
unvisited = {node: float('inf') for node in nodes}
current_distance = 0
unvisited[current] = current_distance
visited, parents = {}, {}
while unvisited:
min_vertex = min(unvisited, key=unvisited.get)
for neighbour, distance in distances[current].items():
if neighbour not in unvisited:
continue
new_distance = current_distance + distance
if unvisited[neighbour] is float('inf') or unvisited[neighbour] > new_distance:
unvisited[neighbour] = new_distance
parents[neighbour] = min_vertex
visited[current] = current_distance
unvisited.pop(min_vertex)
if min_vertex == end:
break
candidates = [node for node in unvisited.items() if node[1]]
current, current_distance = min(candidates, key=lambda x: x[1])
return parents, visitedEste método recebe como argumento o vértice de origem A e o vértice de destino F:
start, end = 'A', 'F'
parents, visited = find_route(start, end)
print(parents) # {'C': 'A', 'B': 'A', 'E': 'C', 'D': 'C', 'F': 'D'}
print(visited) # {'A': 0, 'C': 2, 'B': 5, 'D': 6, 'E': 10, 'F': 10}Agora que temos todos os vértices pais e todos os vértices visitados e a soma de seus pesos, vamos definir um método que irá nos retornar o caminho mais curto:
def generate_path(parents, start, end):
path = [end]
while True:
key = parents[path[0]]
path.insert(0, key)
if key == start:
break
return ' → '.join(path)Este método recebe como argumento os vértices pais e também o vértice de origem A e o vértice de destino F:
path = generate_path(parents, start, end)
print(f'Menor caminho: {path}')Que irá nos retornar: Menor caminho: A → C → D → F.
“A direção das arestas não é importante no algoritmo de Dijkstra. Desde que o grafo de entrada esteja no formato adequado, o algoritmo fornecerá o caminho de saída correto.”
Conclusão
O algoritmo de Dijkstra leva um tempo computacional significativo. A complexidade de tempo em um caso geral é O(V²), onde V é o número de vértices. Isso é melhorado para O(E log V) (onde E é o número de arestas) se a representação do grafo for alterada para listas de adjacências. Embora uma complexidade de tempo polinomial como O(V²) pareça alta, ele é melhor do que algoritmos de força bruta que fornecem tempos computacionais muito maiores.